Event-based Vision Sensor (EVS) 学习笔记
索尼Event-Based Vision Sensor (EVS)介绍。
1. EVS传感器特性
相比于一般的相机以固定频率记录场景的绝对亮度,Event Camear (EC) 每个像素独立地、异步地记录相对亮度变化。其主要有以下几点特性:
- 像素值记录亮度变化。传统相机记录场景的绝对亮度,每一像素记录不同频段的信号强度,由此合成场景图片。而EC记录场景的相对变化,每一像素值为该像素的亮度发生的变化,记录场景的动态变化。
- 异步事件流输出。传统相机的输出是帧率一定的图片,而EC相机的输出是异步“事件流”(a stream of events)。每一“事件”为<时间、位置、亮度变化>组成的三元组。并且,EC相机的像素间是异步的,只要某一像素检测到亮度变化就会发送一个“事件”。
- 时间延迟和时间分辨率在微秒级。EC相机响应单个“事件”和两个“事件”的间隔都在微秒级。这对于低延迟、高速响应系统有着重要意义。
- 信号动态范围广。传统相机的信号动态范围为60dB,超出这个范围会导致信号为0或溢出(欠曝或过曝)。而EC相机的信号范围为140dB,使得它能在白天和晚上都能工作。
- 低功耗。EC相机只记录亮度变化,大大减少数据处理量。
2. 应用场景
- 机器人、可穿戴设备
- 目标识别、追踪
- 手势识别
- SLAM
- 深度估计
- HDR图像重构
- 结构光3D扫描
- …
3. 目前仍面临的困难
- 异步的信息处理。目前大多CV方法都是针对图片的,其空间和时间都是对齐的。而对于“事件流”来说,如何处理异步信息是一个难题。
- 信息缺失与混淆。EC相机的输出是二值化的(“ON”或“OFF”),其能提供的信息很有限。同时,光照和运动变化都会带来亮度的变化,如何在信息缺失的条件下有效解离这两属性是一个难题。
- 如何处理输入噪声。
4. 常见算法与应用
4.1 Event Camera原理
现有的Event Camera多指Dynamic Vision Sensor, DAVIS,即异步记录亮度变化的传感器。对每一像素来说,其记录信号强度的对数变化。如果信号强度变化超过一定阈值,则输出相应的“事件”。每一“事件”由 <(x,y),t,p>组成。其中,(x,y)为像素位置,t为时间,p为1-bit的二值信号,反应信号是增强(“ON”)还是减弱(“OFF”)。
4.2 Input Representation
- 单个“事件”。对“事件”进行逐一处理,如probabilistic filter 和 Spiking Neural Network (SNN)。
- 对“事件”进行批量处理。 根据时间t和位置(x,y)和一定的假设(如运动一致),对一定时间、空间内的“事件”进行统一处理,而后产生输出。
- 将“事件流”转化为2D图片或2D柱状图。通过对“事件”进行计数或累积为2D图像,从而进行处理。这么做的好处有1)2D图像更熟悉;2)在2D图像中,缺失的信息也有意义,通常能反映边界等信息;3)与CNN兼容。
- Time Surface (TS)。TS是一个2D图,其每一像素存储一个对应位置“事件”的时间戳。因此,TS是一个运动历史图(Motion history image),越大的值代表时间上越临近的运动。
- Voxel Grid。为保留时间维度的信息,使用3D柱状图记录“事件”,其中每个voxel代表一个像素和时间间隔。
- 3D点云。将时间作为第3维度,每个“事件”为一个3D点。
- Motion-compensated image。也叫image of warped events (IWE),效果就是锐化边缘,时间对齐。
- Reconstructed Image。
4.3 经典算法
4.3.1 Image of Warped Events (IWE): A Unifying Contrast Maximization Framework for Event Cameras, with Applications to Motion, Depth, and Optical Flow Estimation
这篇文章的核心思路就是,通过按照不同的假设(例如场景运动、目标深度等),将不同时刻的“事件”warp到同一时刻上,由此产生一张image of warped events (IWE)图片。而后通过计算该图片的对比度(contrast),来估算参数。作者将该方法应用于深度、光流预测任务中。
举个直观的例子,一辆拖拉机以一定的速度沿着某一方向匀速行驶,它每隔一段时间就会抛下一块砖头。每个砖头都带有掉落的时间和位置信息。现在我们需要估算出这个拖拉机的运动速度和方向。怎么做呢,首先给拖拉机假设一个运动速度,然后根据运动信息回推每块砖头在$t_r$时刻的位置,然后把$t_r$时刻回推的砖头摞起来,看看有多高。摞起来的砖头最高的那个就是最正确的假设。
对应到EVS中,砖头就是“事件”,所有回推到$t_r$时刻的摞起来的砖头就是IWE,评判砖头高度的方法就是对比度(contrast)。
具体方法如下:

以运动估计为例,首先假定运动参数$\theta$, 而后根据参数将$t_k$时刻的“事件”的位置$x_k$warp到$t_{ref}$时刻上:
\[x_k'=\mathbf{W}(x_k,t_k;\theta)=x_k-(t_k-t_{ref})\theta,\]这里,$\theta=v$是速度向量。基于此,我们生成一个二维数据H,即IWE:
\[H(x;\theta)=\sum_{k=1}^{N}b_k\delta(x-x_k'),\]其中,$N$是“事件”数目,$b_k=1$,$\delta(\cdot)$判定$x_k’$是否落入$x$的周围。
而后,计算H的对比度(即方差):
\[f(\theta)=\sigma^2(H(x;\theta))=\frac{1}{N}\sum_{i,j}(H(i,j)-\overline{H})^2,\]其中,$\overline{H}$为$H$的均值。通过最大化$f(\theta)$,我们就可以得到最优的$\theta$。
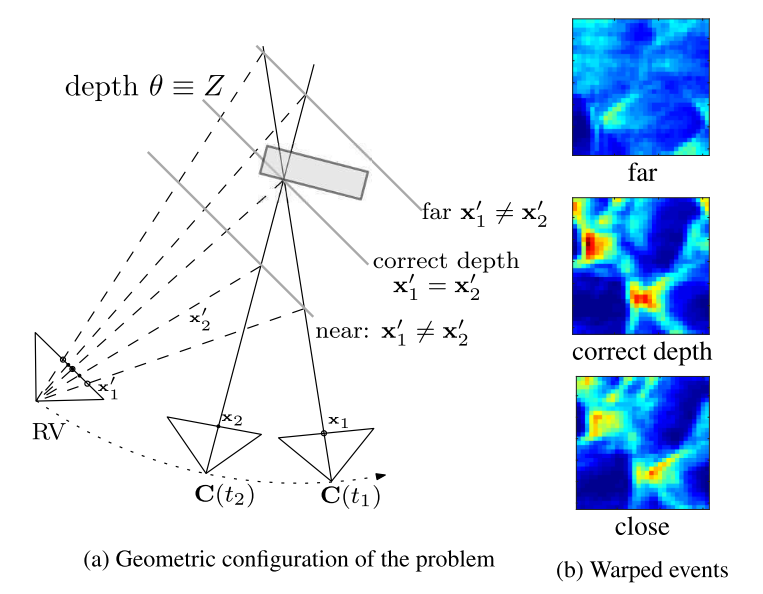
与此类似,深度的估计是通过相机标定和不同时刻的位姿参数,将不同时刻“事件”回推到某一$t_r$时刻,得到IWE。而后计算该时刻IWE的对比度。最大对比度所对应的参数即为最优深度估计。
参考资料
- Gallego, G., Delbrück, T., Orchard, G., Bartolozzi, C., Taba, B., Censi, A., … & Scaramuzza, D. (2020). Event-based vision: A survey. IEEE transactions on pattern analysis and machine intelligence, 44(1), 154-180.